Alternative Statistics

Will Lowe

2019-06-25

This time we’ll use the simple bootstrapping techniques in weat_boot and wefat_boot.

First we load up the package and arrange the graphics

Replicating WEFAT

Same as before to get items and vectors

Now to get bootstrapped differences of cosines. Note that there is no y_name this time and we will get a statistic for each x_name.

This is a bit hard to interpret, so we’ll make a picture

ggplot(res, aes(x = median, y = 1:nrow(res))) +
  geom_point(col = "grey") +
  geom_point(aes(x = diff)) +
  geom_errorbarh(aes(xmin = lwr, xmax = upr), height = 0) +
  geom_text(aes(x = upr, label = Careers), hjust = "left", nudge_x = 0.005) +
  xlim(-0.25, 0.25) +
  ylab("Careers") +
  xlab("Cosine difference (male - female)")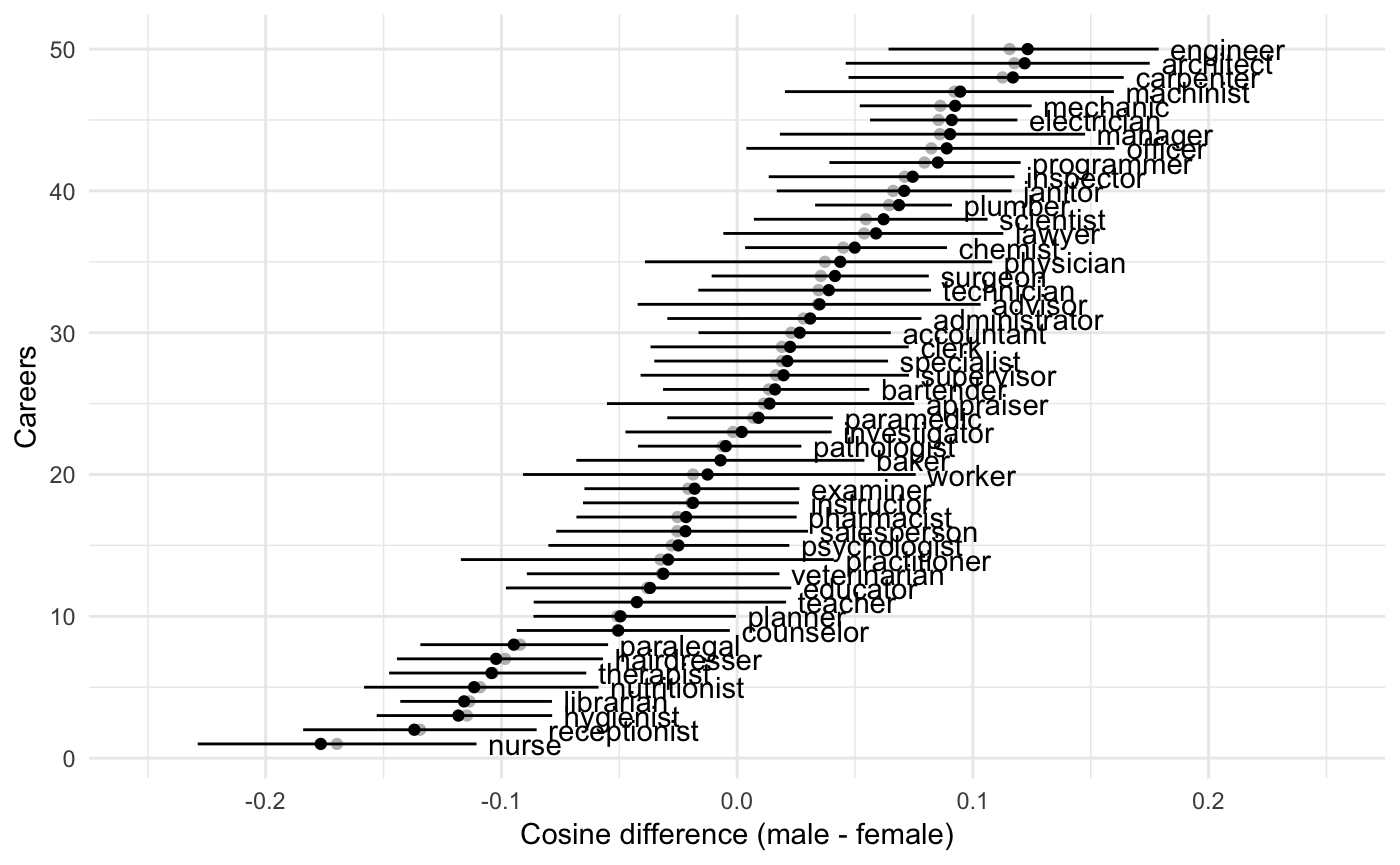

This will work quite generally for WEFATs, but remember to mention the right condition name in geom_text.

I don’t have the male / female proportions for different jobs, so we can’t compare them right now.

The Gender of Androgenous Names

First we get the vector differences

Then we find the gender proportions for each name from the census.
This is most easily done using the gender package, which queries the US Social Security Administration to get the proportion of stated males and females with any particular first name.

This data is bundled with the package, so we’ll join this to res

If you want to do it yourself, e.g. to look at gender over different time periods, or use a different gender source, then

library(gender)

names <- c("Hugh", "Pugh", "Barney")
gender_name_stats <- gender(names)

and replace cbn_gender_name_stats with gender_name_stats.

To see how they relate, we’ll plot proportion male with the diff column of res

ggplot(res, aes(x = proportion_male, y = diff)) +
  geom_hline(yintercept = 0, alpha = 0.5, color = "grey") + 
  geom_point() +
  geom_text(aes(label = AndrogynousNames), hjust = "left", nudge_x = 0.005) +
  xlim(0, 1) +
  xlab("Population proportion male") +
  ylab("Cosine difference (male - female)")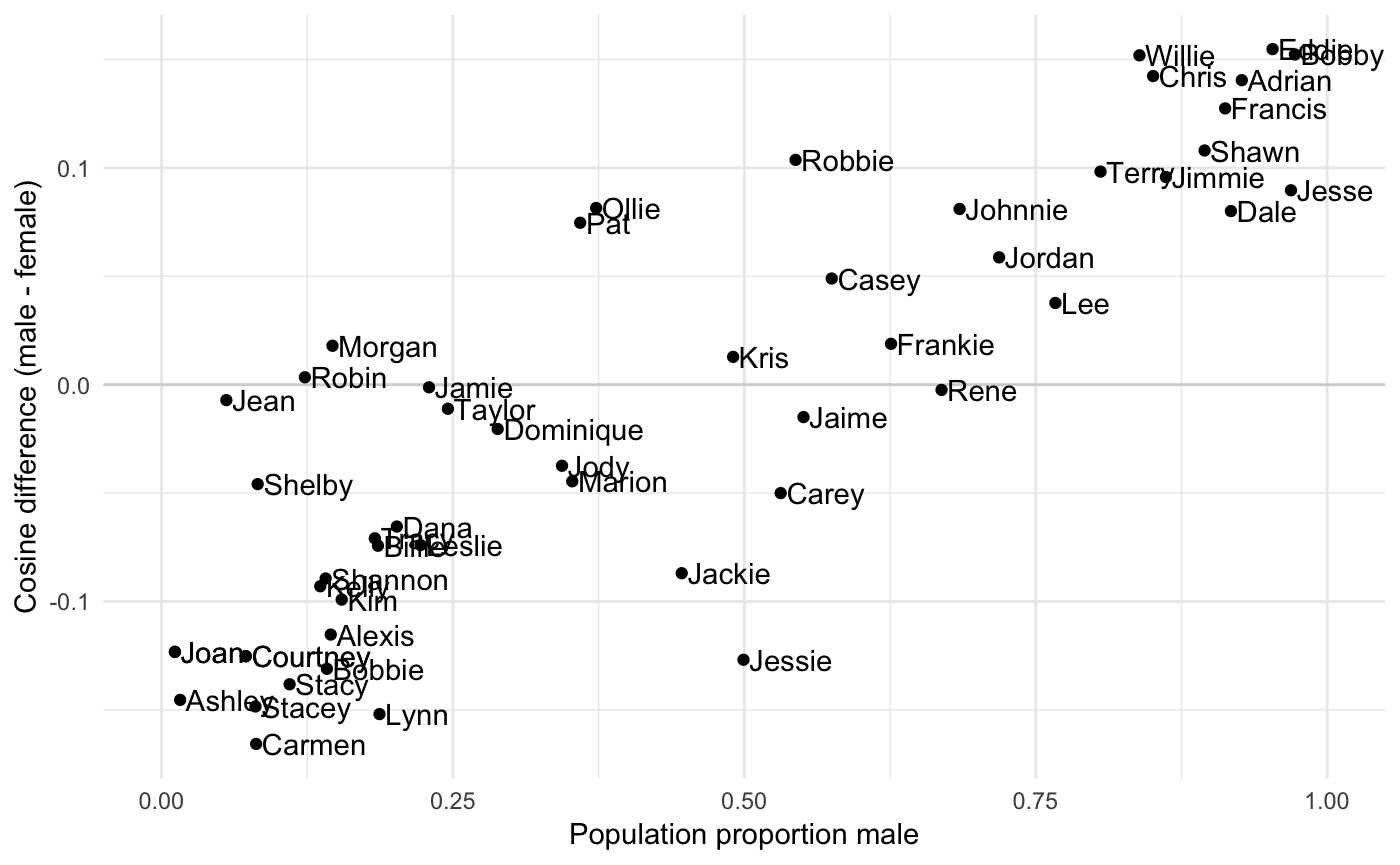

The correlation is